说说吉他泛音的物理学解释，理解驻波波动方程以及泛音是如何产生的
乐理知识
老贾/吉他福 发布时间：2026/2/17 21:57:20 阅读次数：
239
支持
2
中立
3
反对
2
语速：
进度：
吉他琴弦的振动极为复杂，要充分理解这其中的所有奥秘，需要求解大量的微积分方程，但下面的内容仅仅浅尝辄止的说一说这些内容，并不会非常的晦涩难懂 ~~ ^_^ ~~
泛音和驻波
波长频率相同但传输方向相反的两个波叠加，就产生驻波了。
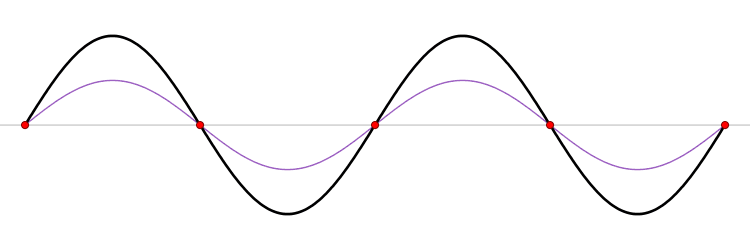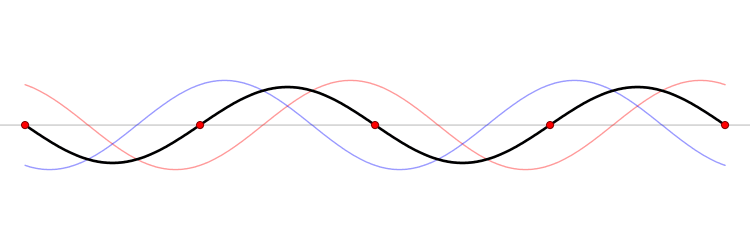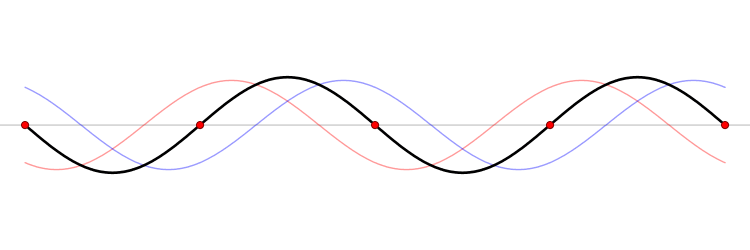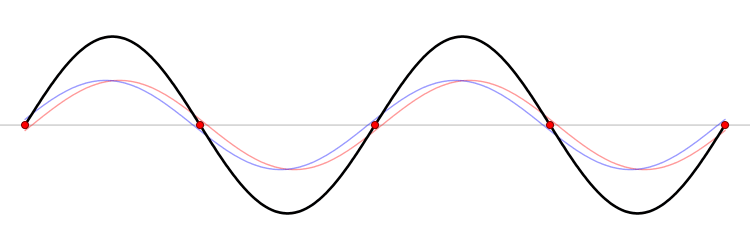
上图中的红色行波很明显是向左传播的，而蓝色的行波是向右的，两个波叠加在一起就变成了黑色的波了，黑色的波形就是典型的驻波。
驻波必需的条件：
一是两端点固定，吉他弦显然是弦枕和弦桥两端固定的。
二是叠加的两个波的频率和传播速度完全相同，且方向相反，在吉他弦上这一点较较难理解，实际的驻波形成非常复杂。
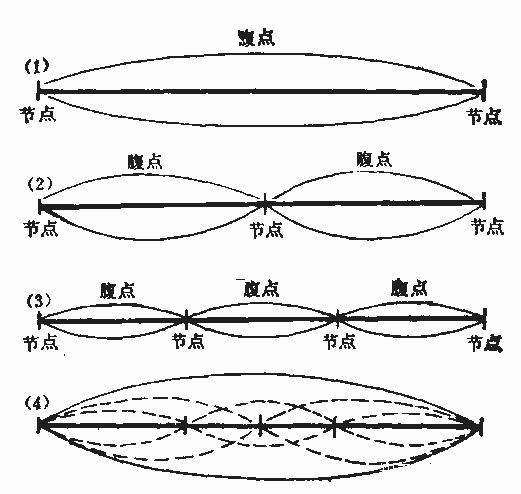
因为吉他弦上的驻波非常复杂，所以分解为大量的倍频的各级泛音的驻波，每一级泛音都是一个驻波。
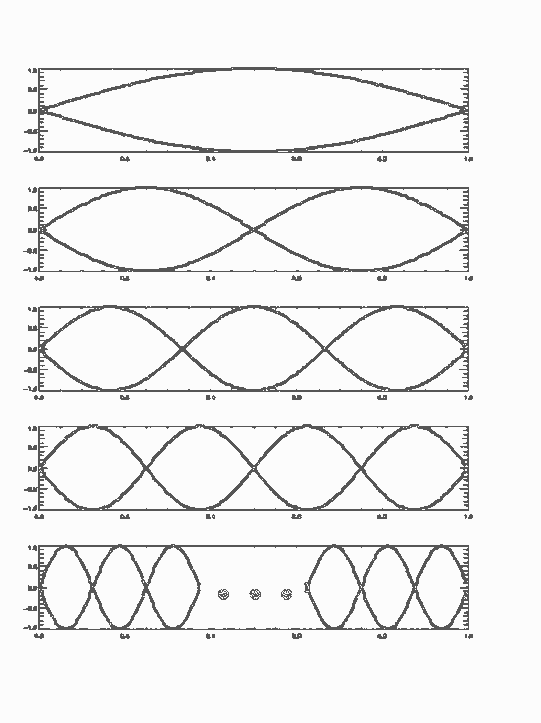
上图中的所有级别泛音会同时存在，并叠加在一起发出声音来。
泛音振动方式就像下图中这样：
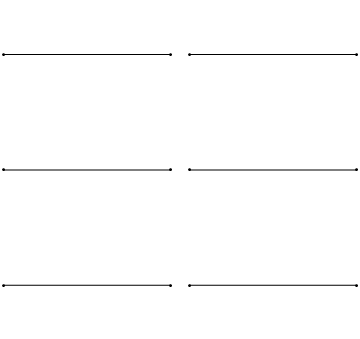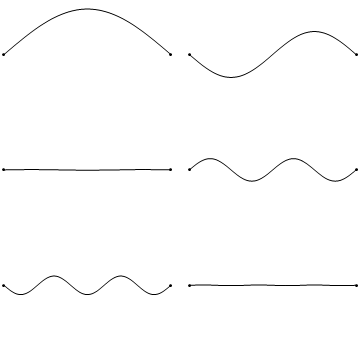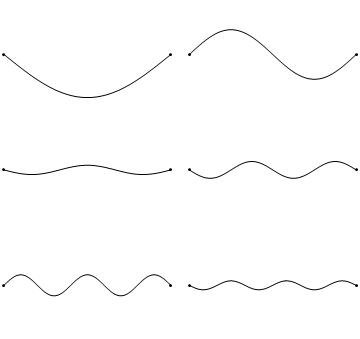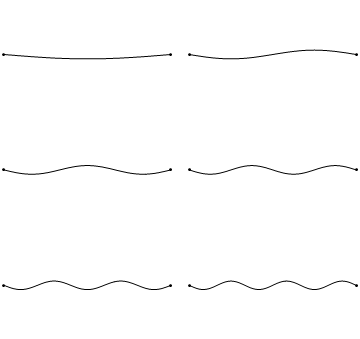
从图中可以看出，级别越高的泛音振动频率越快，当然也就意味着发出的音高就更高了。
驻波的波动方程
下面的波动方程实际上是可以从更本质的牛顿力学微分方程推算求解出来的。
驻波方程：y = y1 + y2 = 2Acos(2πx/λ) * cos(ωt)
A为振幅，λ为波长，ω为角频率
显然的驻波是由y1 y2两列行波相互叠加而成的。
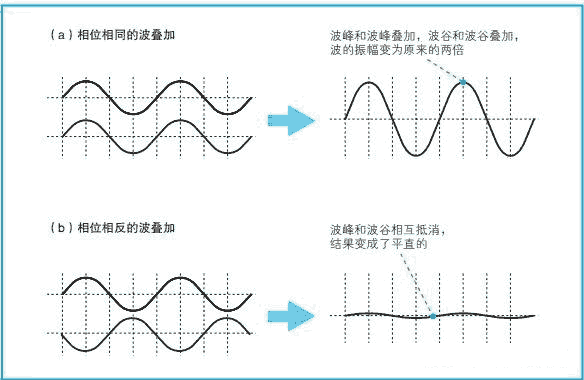
计算过程中，需要用到三角函数的和差化积公式，当然COS和SIN实际上可以相互转换的。
注意：吉他弦上的驻波是波在琴弦的两端不断反射后叠加生成的，很有趣的规律就是波撞在固定端反射的时候是相位相反的，之所以反相是因为不反相就不会叠加为0，而两个端点处肯定是不动的，振幅必须为0..
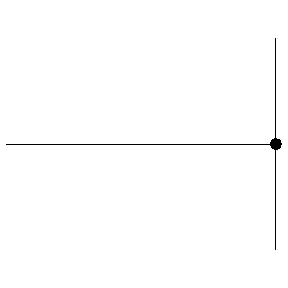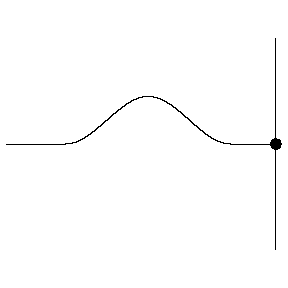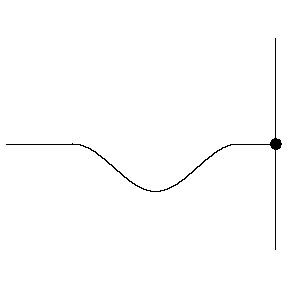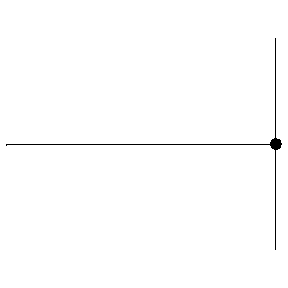
上图中显示了一根绳子上的波撞墙后反射后相位反过来了，先是波朝上鼓起来的，后是波朝下凹下去的。
看起来挺复杂的~~~~ @_@ ~~~~~
泛音的产生
泛音的产生原理可以用傅里叶级数解释，周期函数可以展开为傅里叶级数，计算中要用到大量的积分式，比泰勒麦克劳林等展开式要复杂得多。。。
任何周期函数都可用正弦函数和余弦函数构成的无穷级数来展开，这就是傅立叶级数。
即说展开得到了一系列的正弦或余弦波。。。它是由频率为f,2f,3f,...nf。。基频f称为基音，倍频振动2f,3f,4f,5f,6f,7f...就是泛音了。
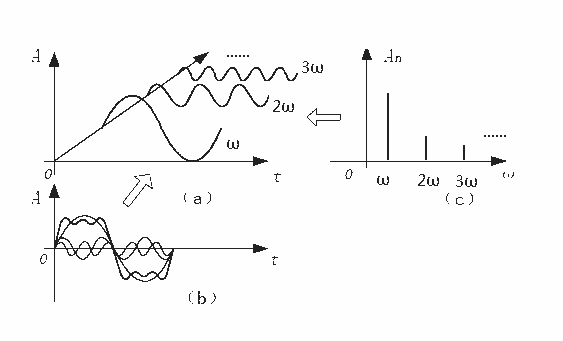
傅里叶级数是正交级数，正交概念是线性代数矩阵数学里的概念。
以此正交的特性，可以轻易提取其中任意一级别的级数项，而完全不会影响其他项。
因为正交性，每一项都相互完全独立，互不干涉，这就解释了为什么一根琴弦上那么多的泛音彼此不会相互影响相互破坏掉，每一级别的泛音都可以独立存在，虽然他们全都在一根弦上振动。。。。
所谓的“正交”，就比如最寻常的直角坐标系，直角坐标系的x轴和y轴就是相互正交的，相互投影都是0，所以正交可以理解为相互垂直的意思，彼此投影都是0的意思。。。。*_* ~~~~
反射波的相位
有趣的物理现象：
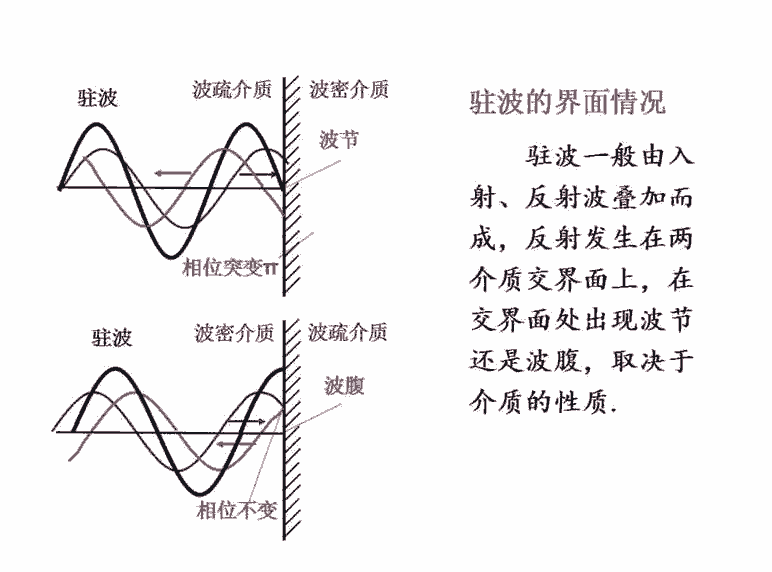
在交界处反射的波，会突然有一个反相（就像上面的绳子波撞墙那样），相位就差了一个半波周期，所以叫做半波损失。
但当波从波密介质入射到波疏介质，这时被反射的波并不反相，分界处不产生相位跃变。
只是对于吉他弦来说肯定是反相的。但无论反相还是不反相都会形成驻波。。。
@_@ 真的好复杂~~~..... 不要泄气，这些知识也不是很重要，知道就行了~~~~ ^o^ !~~~~~
支持👍 2 中立👌 3 反对👎 2
=================================
- - - 新人注册领红包，每天签到领福币 - - -
老贾/吉他福 发布时间：2026/2/17 21:57:20 阅读次数：
239
支持
2
中立
3
反对
2
语速：
进度：
吉他琴弦的振动极为复杂，要充分理解这其中的所有奥秘，需要求解大量的微积分方程，但下面的内容仅仅浅尝辄止的说一说这些内容，并不会非常的晦涩难懂 ~~ ^_^ ~~
泛音和驻波
波长频率相同但传输方向相反的两个波叠加，就产生驻波了。
上图中的红色行波很明显是向左传播的，而蓝色的行波是向右的，两个波叠加在一起就变成了黑色的波了，黑色的波形就是典型的驻波。
驻波必需的条件：
一是两端点固定，吉他弦显然是弦枕和弦桥两端固定的。
二是叠加的两个波的频率和传播速度完全相同，且方向相反，在吉他弦上这一点较较难理解，实际的驻波形成非常复杂。
因为吉他弦上的驻波非常复杂，所以分解为大量的倍频的各级泛音的驻波，每一级泛音都是一个驻波。
上图中的所有级别泛音会同时存在，并叠加在一起发出声音来。
泛音振动方式就像下图中这样：
从图中可以看出，级别越高的泛音振动频率越快，当然也就意味着发出的音高就更高了。
驻波的波动方程
下面的波动方程实际上是可以从更本质的牛顿力学微分方程推算求解出来的。
驻波方程：y = y1 + y2 = 2Acos(2πx/λ) * cos(ωt)
A为振幅，λ为波长，ω为角频率
显然的驻波是由y1 y2两列行波相互叠加而成的。
计算过程中，需要用到三角函数的和差化积公式，当然COS和SIN实际上可以相互转换的。
注意：吉他弦上的驻波是波在琴弦的两端不断反射后叠加生成的，很有趣的规律就是波撞在固定端反射的时候是相位相反的，之所以反相是因为不反相就不会叠加为0，而两个端点处肯定是不动的，振幅必须为0..
上图中显示了一根绳子上的波撞墙后反射后相位反过来了，先是波朝上鼓起来的，后是波朝下凹下去的。
看起来挺复杂的~~~~ @_@ ~~~~~
泛音的产生
泛音的产生原理可以用傅里叶级数解释，周期函数可以展开为傅里叶级数，计算中要用到大量的积分式，比泰勒麦克劳林等展开式要复杂得多。。。
任何周期函数都可用正弦函数和余弦函数构成的无穷级数来展开，这就是傅立叶级数。
即说展开得到了一系列的正弦或余弦波。。。它是由频率为f,2f,3f,...nf。。基频f称为基音，倍频振动2f,3f,4f,5f,6f,7f...就是泛音了。
傅里叶级数是正交级数，正交概念是线性代数矩阵数学里的概念。
以此正交的特性，可以轻易提取其中任意一级别的级数项，而完全不会影响其他项。
因为正交性，每一项都相互完全独立，互不干涉，这就解释了为什么一根琴弦上那么多的泛音彼此不会相互影响相互破坏掉，每一级别的泛音都可以独立存在，虽然他们全都在一根弦上振动。。。。
所谓的“正交”，就比如最寻常的直角坐标系，直角坐标系的x轴和y轴就是相互正交的，相互投影都是0，所以正交可以理解为相互垂直的意思，彼此投影都是0的意思。。。。*_* ~~~~
反射波的相位
有趣的物理现象：
在交界处反射的波，会突然有一个反相（就像上面的绳子波撞墙那样），相位就差了一个半波周期，所以叫做半波损失。
但当波从波密介质入射到波疏介质，这时被反射的波并不反相，分界处不产生相位跃变。
只是对于吉他弦来说肯定是反相的。但无论反相还是不反相都会形成驻波。。。
@_@ 真的好复杂~~~..... 不要泄气，这些知识也不是很重要，知道就行了~~~~ ^o^ !~~~~~
支持👍 2 中立👌 3 反对👎 2
=================================
- - - 新人注册领红包，每天签到领福币 - - -